Pouvez-vous voir à travers ces illusions ?

Les illusions d’optique et les énigmes partagent des vibrations qui se chevauchent. Supercherie mentale, moments « aha », frustration louche. Saviez-vous que la Neural Correlate Society détient un concours annuel pour la meilleure illusion de l’année ? Le gagnant de cette année a créé un modèle LEGO de la plateforme 9 ¾ de Harry Potter, complété par un mur de briques apparemment perméable :

Ce démonstration de miroir soignée se démarque également parmi les finalistes récents. Les énigmes de cette semaine ont un caractère illusoire. J’expliquerai ce que je veux dire dans la rédaction de la solution lundi prochain.

Vous avez raté le puzzle de la semaine dernière ? Vérifiez-le ici, et trouvez sa solution au bas de l’article d’aujourd’hui. Attention à ne pas lire trop loin si vous n’avez pas encore résolu celui de la semaine dernière !

Puzzle n°19 : Illusions mentales

1. 100 fourmis tombent en même temps sur un mètre à des endroits aléatoires. Chaque fourmi commence à marcher vers l’extrémité gauche ou droite du bâton au hasard, à une vitesse d’un mètre par minute. Les fourmis continuent leur parcours choisi, mais chaque fois que deux fourmis entrent en collision, elles inversent immédiatement leur direction et continuent de marcher dans le sens opposé à la même vitesse. Combien de temps cela pourrait-il prendre avant que toutes les fourmis aient quitté le bout du bâton ?

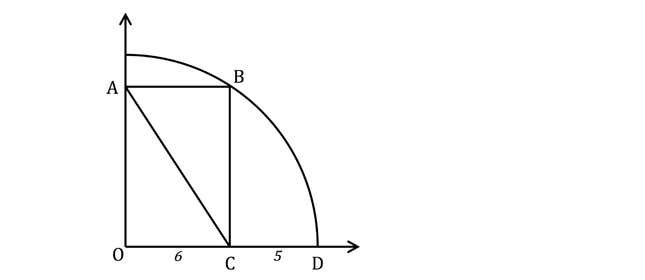
2. Un rectangle est inscrit à l’intérieur d’un quart de cercle centré en O. Trouvez la longueur de la diagonale AC du rectangle.

Je reviens la semaine prochaine avec les solutions et une nouvelle énigme. Connaissez-vous un casse-tête sympa que je devrais aborder ici ? Envoyez-moi un message sur Twitter @JackPMurtagh ou envoyez-moi un e-mail à gizmodopuzzle@gmail.com

Solution de l’énigme n°18 : La longue salle

J’ai fait la semaine dernière question d’entretien d’embauche en finance vous donne du fil à retordre pour votre argent ?

Les carrés parfaits (1, 4, 9, 16, 25, 36, 49, 64, 81 et 100) sont les seules portes qui seront ouvertes à la fin. Bravo à énigme88 pour en déduire la raison.

Pour comprendre pourquoi, rappelons la définition d’un diviseur depuis vos débuts en cours de mathématiques. Les diviseurs d’un nombre sont les nombres qui le divisent uniformément sans reste. Ainsi, par exemple, les diviseurs de 12 sont : 1, 2, 3, 4, 6 et 12. Notez que chaque porte bascule pendant les tours qui correspondent à ses diviseurs (par exemple, lorsque la 8ème personne passe, les portes 8, 16 , 24, 32, etc. sont basculés, tandis que la porte 12 n’est pas touchée car 12 n’est pas divisible par 8). Puisque la porte 12 commence fermée et bascule un nombre pair de fois (elle comporte six diviseurs), elle se terminera en position fermée. La question devient alors : quels nombres ont un nombre impair de diviseurs ?

Les diviseurs ont tendance à venir par paires. 1 se multiplie par 12 pour obtenir 12, donc 1 et 12 sont tous deux diviseurs. 2 se multiplie par 6 pour obtenir 12, ils sont donc tous deux diviseurs, et ainsi de suite. Ainsi, les seuls nombres dont les diviseurs ne viennent pas tous par paires sont les nombres qui peuvent être obtenus en multipliant un nombre. avec lui-même. Par exemple, les diviseurs de 16 sont 1, 2, 4, 8 et 16. 1 s’apparie avec 16, 2 s’apparie avec 8 et 4 n’a pas de partenaire car 4 est multiplié par lui-même pour égaler 16. Donc les carrés parfaits sont exactement ces nombres avec un nombre impair de diviseurs et ce sont les portes qui finissent par s’ouvrir.

J’aime ce puzzle car les carrés parfaits semblent sortir de nulle part. Il n’y en a aucune odeur dans la configuration. Beaucoup de gens sont familiers avec les nombres au carré, mais je soupçonne que leur caractérisation comme étant les seuls nombres avec un nombre impair de diviseurs sera nouvelle pour de nombreux lecteurs.